About me
I specialize in mathematical and computational hydrogeology. My major interests are inverse problems, random walk methods, quantifying uncertainty due to unresolved heterogeneity, and use of machine learning for predictive modelling and upscaling. I have done practical modelling covering a wide variety of topics in subsurface solute transport: these include chlorinated solvents, radionuclides, supercritical CO2, (bio-)reactive transport, and tracer test interpretation.
In 2018 I was appointed Senior Lecturer in the Zuckerberg institute for Water Research at Ben-Gurion University of the Negev. I previously worked in the Computational Earth Science Group at Los Alamos National Laboratory, where I led development of the CHROTRAN software and performed inverse modelling research. Prior to this, I worked as a postdoc with Brian Berkowitz at the Weizmann Institute, focusing on CTRW methods and reactive transport. I completed my PhD at Queen's University, where I held an Alexander Graham Bell Canada Graduate Scholarship.
A native of Toronto, I now live at Midreshet Ben-Gurion with my wife and twin boys. In my free time, when not playing with my kids, I pursue my interests in ambient and electronic music, parser-based interactive fiction (AKA text adventure games), and reading a wide range of non-fiction.

Research
The following projects are those I am currently focused on. While they do not give a comprehensive picture of my research activities (see also my publications), I think they give the flavour of my work:
Upscaling of reactive transport models
A major challenge when trying to model subsurface reactive transport is that the diffusion timescale tends to greatly exceed the reaction timescale. This results in the formation of reactant islands, with reactions spatially limited to occur at interfaces that make up only a small portion of the domain. This makes reaction kinetics computed under well-mixed laboratory conditions of limited applicability in the subsurface. Modelling needs to predict, not just to fit observations post hoc. This requires quantifying the dynamics of island growth and relating these to measurable parameters that describe subsurface heterogeneity. Using a combination of analytical techniques and machine learning, I am developing upscaled effective reaction rate models with predictive power.

Growth of solute islands over time (increasing from top to bottom) as two chemical species, A and B, undergo a bimolecular annihilation reaction (A + B → 0) in a heterogeneous, periodic velocity field. The greyscale images show the local value of the difference in concentration, CA - CB: dark colour indicates large positive values and white colour indicates large negative values. Island growth, with corresponding shrinkage of interfacial length, is clearly visible.
Adjoint-state error envelope calibration
The subsurface is a data-poor environment, described by three-dimensional parameter fields that are greatly underdetermined by any realistically-obtainable quantity of measurements. The question of how poor this characterization is, and its implications for quantities of interest, are generally not addressed as the parameter space is too large to reasonably explore. Adjoint-state gradient-descent methods can help solve this problem because their computational complexity is determined by the number of observations, rather than the number of parameters. It thus becomes simple to compute an ensemble of locally-optimal parametrizations for numerous equiprobable initial guesses, and to numerically obtain error envelopes. I am developing a Python package using the FEniCS library to enable these analyses.
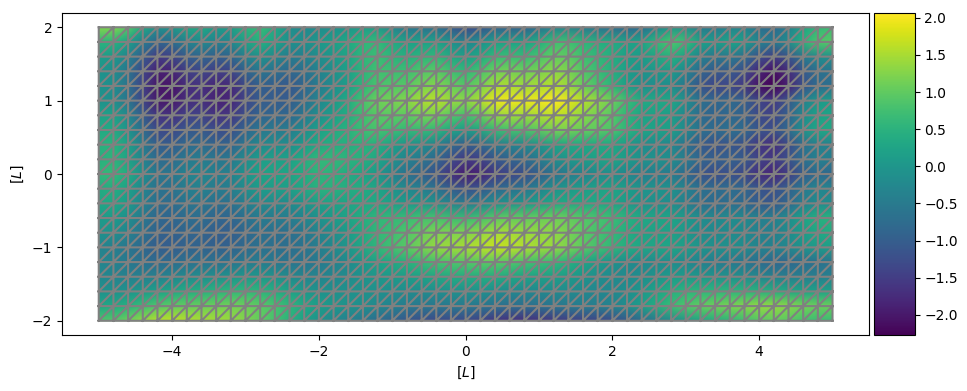
Example of a target transmissivity field given a finite-element representation using FEniCS. Using head (and optionally, velocity and/or local conductivity) measurements at a limited number of spatial locations, the transmissivity field and its boundary conditions is reconstructed using the adjoint-state method.
Supercritical CO2 injection in heterogeneous aquifers
The dynamics of supercritical CO2 injection are governed by a non-linear transport equation and consequently must be studied numerically. Numerical models of subsurface CO2 injection commonly assume that CO2 is introduced into an initially hydrostatic, homogeneous domain. Using PFLOTRAN, I have developed the capability to relax these assumptions, and to reveal the effect that combined heterogeneity and flow have on the uptake of CO2. The ultimate goal of this research is to optimize engineered injection schemes for reliability and uptake rate.
Simultaneous simulations of supercritical CO2 uptake in each of ten statistically-identical, multi-Gaussian hydraulic conductivity field realizations. (Realizations are 2D and seen from the side.) The impact of the (very mild, σln K=1) heterogeneity seen here is notable. Its effect is strongly magnified with increased correlation lengths and left-to-right hydraulic gradient (not shown here).
Aurora software
In recent academic research on solute transport, it has become common to employ sophisticated solute transport models. These include continuous-time random walk (CTRW), fractional advection-dispersion, and subordination approaches. However, the groundwater flow models with which these are coupled tend to be quite simple. Conversely, hydrogeologic practitioners tend to employ basic transport models based on the advection-dispersion equation, but to implement complex flow models in MODFLOW. I am developing the Aurora software to bridge the gap between these worlds, by allowing CTRW-based particle tracking to be performed on arbitrary velocity fields produced by MODFLOW. You can explore its Git repository here.
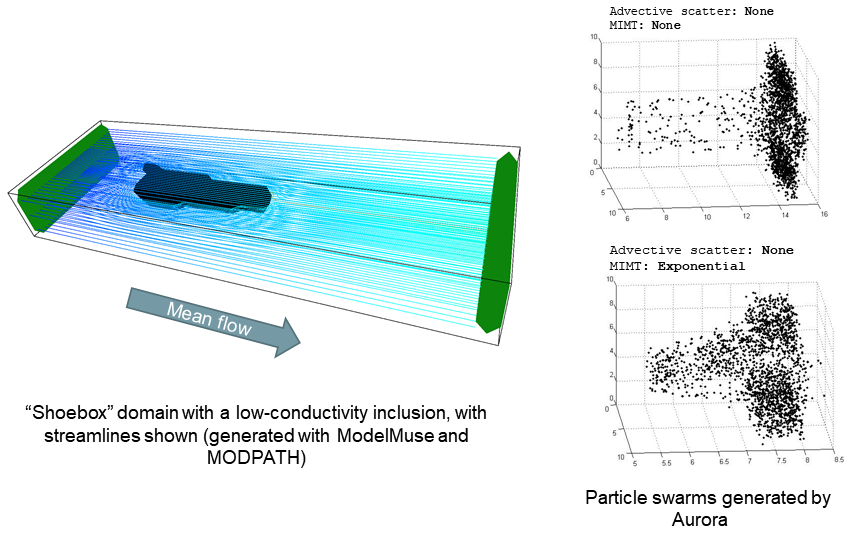
Example of two sets of Aurora particle tracking results (shown at right) for different mobile-immobile mass transfer regimes. Both of these were generated using the same MODFLOW-derived heterogeneous flow field (shown at left).
Student Opportunities
I am actively seeking MSc and PhD students who are skilled in applied mathematics and computer programming. The work in my lab is interdisciplinary, so a variety of backgrounds may provide good preparation, including physics, mathematics, engineering, and geosciences. Regardless of background, strong quantitative skills (whether acquired formally or on your own) and excellent problem-solving abilities are musts. In return for your skills, I offer a full stipend, a collaborative, one-on-one working environment, and a lab featuring exclusive-use high-performance computing equipment that includes a 64-core AMD EPYC compute server and high-end CUDA GPGPU capabilities.
My intent is to operate with a modest number of strong, independent-minded graduate students, and to be actively involved in the research (with doctoral students taking the lead in their own research programs, of course). Where a choice exists, my preference is to focus on higher-impact publications rather than a larger number of lower-impact ones.
At the PhD level, projects could include development of closure relationships for upscaled effective reaction rates in heterogeneous velocity fields; and mathematical investigation of the impact of model error in inverse problems / optimal model selections.
At the MSc level, projects could include exploration of the effects of subsurface heterogeneity on CO2 dynamics using PFLOTRAN; development and application of the Aurora software; and prediction of error envelope size as a function of data quantity for hydrogeologically relevant parameters.
I also have some flexibility to supervise unique theses that do not directly tie into the projects I mentioned above, as long as they do not require substantial equipment purchases (i.e., they need to be modelling based). If you can demonstrate a strong record, have an idea you are excited about that lies at the nexus of hydrogeology, applied mathematics, and scientific computing, and you think our interests may match, please don't hesitate to get in touch.
Publications
Refereed journal articles
D.K. Burnell, J. Xu, S.K. Hansen, L.S. Sims and C.R. Faust (2018). A Practical modelling Framework for Non‐Fickian Transport and Multi‐Species Sequential First‐Order Reaction. Groundwater 56(4), pp. 524-540.
S.K. Hansen, C.P. Haslauer, O.A. Cirpka and V.V. Vesselinov (2018). Direct breakthrough curve prediction from statistics of heterogeneous conductivity fields. Water Resources Research 54(1) pp. 271-285.
S.K. Hansen, J. He and V.V. Vesselinov (2018). Characterizing the impact of model error in geophysical time series recovery inverse problems. Advances in Water Resources 111, pp. 372-380
S.K. Hansen, and V.V. Vesselinov (2018). Local Equilibrium and Retardation Revisited. Groundwater 56(1), pp. 109-117.
V.G. Stanev, F.L. Iliev, S. Hansen, V.V. Vesselinov, B.S. Alexandrov (2018). Identification of release sources in advection–diffusion system by machine learning combined with Green’s function inverse method. Applied Mathematical Modelling 60, pp. 64-76.
S.K. Hansen, S. Pandey, S. Karra and V.V. Vesselinov (2017). CHROTRAN v1.0: a mathematical and computational model for in situ heavy metal remediation in heterogeneous aquifers. Geoscientific Model Development 10, pp. 4525-4538.
S.K. Hansen, V.V. Vesselinov, Z. Lu, P.W. Reimus (2017). Inferring subsurface heterogeneity from push-drift tracer tests. Water Resources Research 53(7), pp. 6322-6329.
D.K. Burnell, S.K. Hansen and J. Xu (2017). Transient modelling of non-Fickian transport and first-order reaction. Advances in Water Resources 107, pp. 370-392.
S.K. Hansen, B. Berkowitz, V.V. Vesselinov, D. O'Malley and S. Karra (2016). Push-pull tracer tests: their information content and use for characterizing non-Fickian, mobile-immobile behavior. Water Resources Research 52(12), pp. 9565-9585.
S.K. Hansen and V.V. Vesselinov (2016). Contaminant point source localization error estimates as functions of data quantity and model quality. Journal of Contaminant Hydrology 193, pp. 74-85.
B. Berkowitz, I. Dror, S.K. Hansen, and H. Scher (2016). Measurements and models of reactive transport in geological media,. Reviews of Geophysics 54(4), pp. 930-986.
S.K. Hansen (2015). Effective ADE models for first-order mobile-immobile solute transport: limits on validity and modelling implications. Advances in Water Resources 86 Part A, pp. 184–192.
S.K. Hansen and B. Berkowitz (2015). Integrodifferential formulations of the continuous-time random walk for solute transport subject to bimolecular A + B → 0 reactions. Physical Review E 91, 032113.
S.K. Hansen and B. Berkowitz (2014). Interpretation and nonuniqueness of CTRW transition distributions: insights from an alternative solute transport formulation. Advances in Water Resources 74, pp. 54–63.
S.K. Hansen, H. Scher and B. Berkowitz (2014). First-principles derivation of reactive transport modelling parameters for particle tracking and PDE approaches. Advances in Water Resources 69, pp.146–158.
S.K. Hansen and B.H. Kueper (2014). A new model for coupled multicomponent NAPL dissolution and aqueous-phase transport, with application to creosote dissolution in discrete fractures. Water Resources Research 50, pp. 58–70.
S.K. Hansen (2013). Semianalytic solution for transport of a two-member decay chain in discrete parallel fractures. Water Resources Research 49, pp. 6105–6110.
S.K. Hansen (2011). On the effects of a totally reflecting barrier on an unbiased 1D random walk. Physica Status Solidi B 248(9), pp. 2112–2119.
S.K. Hansen and B.H. Kueper (2011). Forensic misidentification of Aroclor sources in fractured bedrock due to "chromatographic" polychlorinated biphenyl (PCB) congener separation. Environmental Forensics 12(1), pp. 25-34.
S.K. Hansen and B.H. Kueper (2009). An efficient method for asymptotic solution to some linear PDEs having arbitrary time-varying type I boundary conditions. Applied Mathematics and Computation 207(1) pp. 273-278.
S.K. Hansen and B.H. Kueper (2007). An analytical solution to multi-component NAPL dissolution equations. Advances in Water Resources 30(3), pp. 382-388.
R.K. Rowe, T. Mukunoki, R.J. Bathurst, S. Rimal, P. Hurst and S. Hansen (2007). Performance of a geocomposite liner for containing Jet A-1 spill in an extreme environment. Geotextiles and Geomembranes 25(2), pp. 68-77.
Technical reports
S.K. Hansen, H. Boukhalfa, S. Karra, D. Wang and V.V. Vesselinov (2017). Chromium (VI) reduction in acetate-and molasses-amended natural media: empirical model development. Report no. LA-UR-17-30690, Los Alamos National Laboratory (LANL), Los Alamos, NM.
S.K. Hansen, S. Pandey, S. Karra and V.V. Vesselinov (2017). CHROTRAN, 1.0. Report no. CHROTRAN; 005231MLTPL00 C17061, Los Alamos National Laboratory (LANL), Los Alamos, NM.
Connect
If your interest is primarily in my work, you can find my papers listed above, or check out my profiles on Google Scholar, ResearchGate, ORCID, or LinkedIn. You can find some of my software at Gitlab. If you want to contact me personally regarding research, student opportunities, or consulting engagements, contact information follows (email is usually best):
| skh@bgu.ac.il | |
| Office | Rm. 101, Zuckerberg Institute for Water Research Jacob Blaustein Institutes for Desert Research Ben-Gurion University of the Negev Sede Boqer Campus, 8499000, Israel |
| Phone | +972-8-65-63464 |